I attended and presented the following poster. LOCC only holds if one demands that in a classical – quantum connection that QM is not altered.
Archives For November 30, 1999
Can QM be correct? Like any other theory, it will be bound to fail.
World Quantum Day is April 14th, and as such I’d like to post this idea.
Dark energy and dark matter – the entire dark sector – is composed of ‘quantum mechanics’.
This is pretty far out, but it is World Quantum Day!
Further details/assumptions.
- QM is de Broglie / Bohm mechanics or some similar phenomena
- This requires a guiding potential, and every other potential we have found needs a field.
- This field sticks around matter (EG dark matter),
- Some leaks out, becomes free, which is dark energy.
Expanded…
QM is de Broglie/Bohm
A popular enough opinion, but in this case perhaps we would need the wave function to live in 3D space, instead of that pesky Hilbert one. The wave function in proper de-Broglie Bohm has no mass, obvisously, so this is really a de-Broglie Bohm LIKE theory.
Guiding field
The Quantum Potential doesn’t feel field like a normal field – it’s more of a steering thing, but if you look at Couder/Bush experiments and theory, it’s possible for this guiding wave function field to be a real valued, normal excitation, which instead of guiding particles with its strength, guides them with its form.
Wave functions hang around matter
Duh – that’s the point of QM! When you think about it though, this sort of idea would require the wave functions to have a mass of up to 100 (average is about 6) times the mass of the matter they control. Furthermore, this QM wave function field would have more mass the more rarefied the baryons are. Think of a QM system (single atom) needing more energy to probe larger spaces around it to ensure QM behaviour still happens. Of course, at some point, matter will become too rarefied to support QM, at which point QM might break down. Since DM density is typically GeV/cm3 and DM seems to hang on until baryon densities are lower than that, in ordinary laboratory matter, (ie a 1cm lump of steel), ‘DM’ Quantum waves might only have a mass of a few hundred GeV, undetected in terrestrial experiments. But rarefy that lump to say 1GeV/cm^3 and the QMDM will start to out mass the matter. Where does the QMDM energy come from? It comes from the QM waves (’empty Bohm waves if you will) around us. This QMDM is extremely reactive to matter – it’s dragged along (hence Renzo’s rule from MOND) and thus forms dark matter.
Dark Energy
But think of what happens at the edge of a galaxy. The matter there gets rarefied to the point of not being able to keep the QMDM energy around, and some of it slowly leaks out, providing for dark energy to emerge as a significant energy in the as the Universe ages past a few billion years old.
Rather crazy?
Pointing out that looking for particles as the source of the dark sector is kinda limiting. I also do personally back de-Broglie Bohm theory for QM, and an energy content to quantum mechanics. Considering QM as requiring energy to function is IMO not all that big of a stretch.
John discusses how gravitational waves might be the mechanism for pilot wave mechanics.
Continue Reading...
While the physics media, popular opinion and generally accepted lecturers says things like ‘GR is wrong because singularities’, the physical and theoretical facts suggest very strongly the opposite.
Continue Reading...
I presented at the APS 2021 2021
The recent experimental proposals by Bose et al. and Marletto et al. (BMV) outline a way to test for the quantum nature of gravity by measuring the gravitationally induced differential phase accumulation over the superposed paths of two ∼10^-14kg masses.
This work predicts the outcome of the BMV experiment in Bohmian trajectory gravity – where classical gravity is assumed to couple to the particle configuration in each Bohmian path, as opposed to semi-classical gravity where gravity couples to the expectation value of the wave function, or of quantized gravity, where the gravitational field is itself in a quantum superposition.
In the case of the BMV experiment, Bohmian trajectory gravity predicts that there will be quantum entanglement. This is surprising as the gravitational field is treated classically.
T C Andersen 2019 J. Phys.: Conf. Ser. 1275 012038 – 9th International Workshop DICE2018 : Spacetime – Matter – Quantum Mechanics
Abstract. The recent experimental proposals by Bose et al. and Marletto et al. (BMV) outline a way to test for the quantum nature of gravity by measuring gravitationally induced differential phase accumulation over the superposed paths of two ∼ 10−14kg masses. These authors outline the expected outcome of these experiments for semi-classical, quantum gravity and collapse models. It is found that both semi-classical and collapse models predict a lack of entanglement in the experimental results. This work predicts the outcome of the BMV experiment in Bohmian trajectory gravity – where classical gravity is assumed to couple to the particle configuration in each Bohmian path, as opposed to semi-classical gravity where gravity couples to the expectation value of the wave function, or of quantized gravity, where the gravitational field is itself in a quantum superposition. In the case of the BMV experiment, Bohmian trajectory gravity predicts that there will be quantum entanglement. This is surprising as the gravitational field is treated classically. A discussion of how Bohmian trajectory gravity can induce quantum entanglement for a non superposed gravitational field is put forward.
This paper is a result of a talk I gave at DICE2018. The trip and the talk allowed me to sharpen the math and the arguments in this paper. I’m convinced that the results of a BMV like experiment would show these results – namely that gravity violates QM! Most physicists are of course on the opposite side of this and would assume that QM would win in a BMV experiment.
For those of the main camp, this paper is still important, as it describes another way to approximate quantum gravity – one that works better than the very often used Rosenfeld style semi-classical gravity. Sitting through talks where researchers use the semi-classical approximation in order to do sophisticated quantum gravity phenomenology has convinced me that often the results would change significantly if they had of used a Bohmian trajectory approach instead. The chemists figured this out a while ago – a Bohmian approximation is much more accurate than semi-classical approximations.
In some sense semi-classical gravity seems more complicated than Bohmian trajectory gravity, as in semi-classical gravity the gravitational field has to somehow integrate the entire position space of the wave function (a non local entity) in real time (via the Schr ̈odinger – Newton equation), in order to continuously use the expectation value as a source for the gravitational field. In Bohmian mechanics, the gravitational field connects directly to an existing ’hidden’ particle position, which is conceptually simpler.
22nd International Conference on General Relativity and Gravitation
I am attending GR22 in Valencia Spain, to present a poster and also take part in the talks. I will be presenting a poster based on this paper (soon to be published) from a talk I gave at DICE2018.
What the paper and poster argue is that in the BMV experiment, observing entanglement is not enough to show that gravity is quantum. I do this by showing that a classical gravitational field coupled to the Bohmian trajectories of the individual particles will show entanglement.
The conference looks like its going to be interesting to attend.
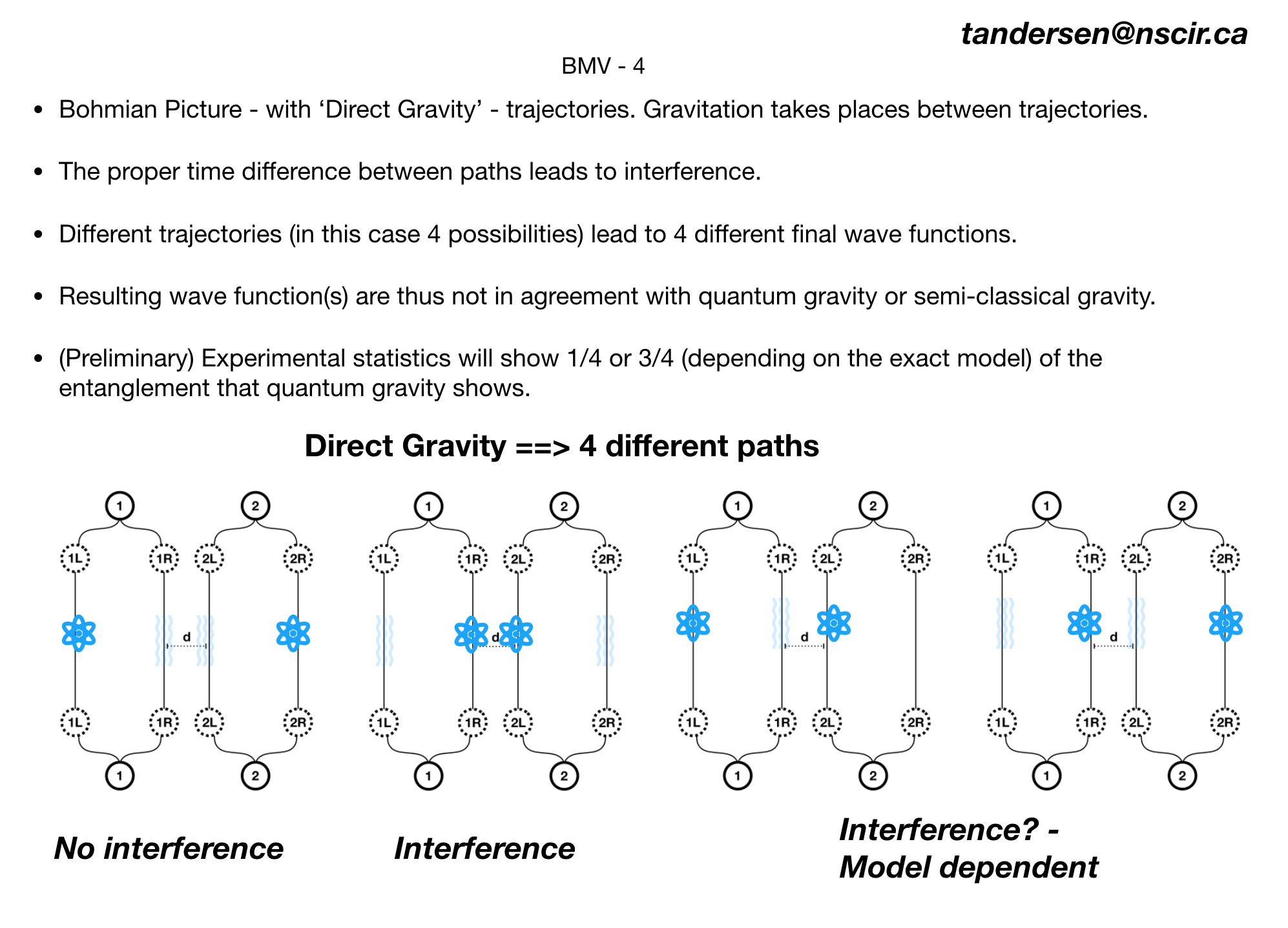
The image at the top shows 4 runs of the BMV experiment, with all 4 Bohmian particle trajectory combinations shown. There is entanglement generated 1/4 of the time, when the experiment happens to look like the 2nd diagram from the left.
The poster is 90 x 200cm, available in real 3D, if you visit Valencia From July 7-12 2019 :-)
The BMV experiment sets out to show that gravity is quantized. If gravity is quantized, we expect to be able to form a gravitational field into a superposition, so that fundamentally the gravitational field is not certain at one spacetime point. Trying to come up with a theory of gravity that can be in a quantum superposition, while still working for all present tests of Einstein’s General Relativity has proved impossible so far, despite thousands of very smart people working over 50 years on the problem.
Perhaps gravity cannot be quantized. With Bohmian trajectory gravity, gravity is not quantized and has a well-defined connection to the sub-atomic particles.
If gravity is not quantized, all sorts of assumptions about quantum mechanics suddenly fail, as an unquantized gravity allows one to cheat behind the back of quantum mechanics. This is a large part of the reason why many people think gravity must be quantized. I’m not in the gravity must be quantized group, mostly because I think it just won’t work.
as revealed by J.S. Bell and experimental results.
Consider the following facts.
- The experimental record shows that the Lorentz transformations and special and general relativity all work remarkably well, from galaxies and indeed the structure of the Universe on down to scales probed by CERN.
- Locality is demonstrated in virtually all experiments conducted to date. This holds across fields such as fluid dynamics, radiation fields, etc. We have local causality.
- Quantum experiments such as those done by Aspect and later show that not everything is local – we have non-local effects. The wavefunction collapse is instant, etc. This worried Einstein.
Given the above facts, the simplest spacetime I can come up with looks roughly like this:
So this spacetime, which is not new, ( Wheeler had similar ideas), seems to cover our knowledge about the logical structure of quantum mechanics and general relativity. Until someone comes up with something better, this is what I use.
Causality vs locality vs non-signalling
- Spacetime is locally casual. Einsteins equations show us how things need to touch (with light or gravity waves, etc) in order to interact.
- Locality is therefore local in nature only.
- non-signalling holds today, but there seems to be no reason for it. We have a connection, we just need to figure out how to use it.
- Spacetime is multiply connected, which means it is not globally localized. Events can interact outside of their past light cones.
Conclusion
This is how our universe operates: we feel everything locally causal. But experiment shows some non-local (in the global sense) connections.
I think that the biggest news in a while in quantum mechanics is newly forming ability of experimenters to do quantum experiments with gravity. A fine example of an experiment already done is Phase Shift in an Atom Interferometer due to Spacetime Curvature across its Wave Function by Asenbaum et al. They conclude:
Therefore, the phase shift of this interferometer is not determined by the local acceleration along a single populated trajectory, demonstrating that the atomic wavefunction is a nonlocal probe of the spacetime manifold [34].
Thus they have experimentally shown that wave functions feel gravity pretty much where they ‘are’ in real space ( try not to think of configuration space at this point! ). No one really doubted this would happen. Still, it leads one to wonder what about the other side – the backreaction – to this. Do the atoms in the Asenbaum experiment source gravity in the same way they detect it? It would seem obvious that they should, but no one has done an experiment to verify this (see later in this article).
A proposal in the opposite spirit to the above results is given by Kafri, Taylor, and Milburn (KTM) in A classical channel model for gravitational decoherence. KTM posits a way for the gravity to be sourced as follows:
That is, the gravitational centre of mass coordinate,xi, of each particle is continuously measured and a classical stochastic measurement record, Jk(t), carrying this information acts reciprocally as a classical control force on the other mass.
In other words in the KTM model, the source and detection channels for a particle are both as in semi-classical gravity. The expectation value of the particle’s is the mass location for both source and detection.
You can sense that the Asenbaum experiment shows KTM does not work – the experiment shows that atom, which is in a dual humped wave function with a separation of centimeters cannot be seeing only the average field – the wave function senses the curvature. The paper by Altamirano, Corona-Ugalde, Mann, and Zych Gravity is not a Pairwise Local Classical Channel , confirm these feelings about KTM – like theories. They don’t work.
Here we show that single-atom interference experiments achieving large spatial superpositions can rule out a framework where the Newtonian gravitational inter-action is fundamentally classical in the information-theoretic sense: it cannot convey entanglement. Specifically, in this framework gravity acts pairwise between massive particles as classical channels, which effectively induce approximately Newtonian forces between the masses.
So gravity is not truly semi-classical. No surprise to me, or to the quantum gravity workers (LQG, String Theory, etc). What many/most quantum gravity people like to think, however, is that KTM or similar (Diosi – Penrose), Rosenfeld like semi-classical gravity basically exhaust the spectrum of classical gravity theories.
The BMV Experimental Proposals
The papers describing the BMV experiments by Bose et al., Marletto and Vedral, and Christodoulou and Rovelli.
These proposed experiments are in some ways similar to the Asenbaum experiment described above, but instead of atoms, small particles like micro diamonds are prepared in position-dependent superpositions, and instead of a huge mass of lead, two diamonds are dropped near each other, so they can feel the gravitational effect of the other also in a position superposition diamond. The promise of these experiments is tremendous – if successful they might show that gravity is quantized: Christodoulou and Rovell state
...detecting the [BMV] effect counts as evidence that the gravitational field can be in a superposition of two macroscopically distinct classical fields and since the gravitational field is the geometry of spacetime (measured by rods and clocks), the BMV effect counts as evidence that quantum superposition of different spacetime geometries is possible, can be achieved..
A problem I see in these BMV papers is that they all use the predictions of semi-classical theories (not KTM but semiclassical as a source only) as a classical test case, without much thought to the predictions of other ‘classical’ theories of gravity. The possibilities are many and the experimental consequences are not simple.
Bohmian Trajectories and General Relativity
There have been some papers over the years touting the usefulness of the Bohmian trajectory viewpoint as a better approximation to classical field – quantum system interaction. Usually, the case for using Bohmian trajectories is one of computational or conceptual efficiency, but as Ward Struve in Semi-classical approximations based on Bohmian mechanics puts it:
Finally, although we regard the Bohmian semi-classical approximation for quantum gravity as an approximation to some deeper quantum theory for gravity, one could also entertain the possibility that it is a fundamental theory on its own. At least, there is presumably as yet no experimental evidence against it.
The BMV experiment with Bohmian trajectories
The interpretation of the BMV experiment if one assumes Bohmian trajectories are ‘real’ results in the following conclusions:
- Each run of the experiment has particles in any one of 4 configurations, – the trajectories.
- There is no superposition of gravitational fields – each run has a different gravitational field configuration.
- The resulting experimental statistics show entanglement – even though gravity is classical throughout.
The last point is the most surprising. We look at why an experimenter will see entanglement with Bohmian trajectories.
At the heart of the argument is the fact that while these Bohmian trajectories look very classical, they are actually quantum – more clearly subquantum aspects of (Bohm/de Broglie) quantum theory. So we have a situation where we can get behaviour very similar – ( i.e. showing entanglement ) to quantum gravity for the BMV experiment by using classical gravity coupled to Bohmian trajectories, where there is a superposition of gravitational fields – but only in the boring classical histories of the experiment viewpoint. Since the experimenter has only histories to look at, showing that the gravitational field was in a superposition requires more than merely observing some level of entanglement in the BMV experiment.
This is a paper version of the poster I presented at EmQM17 in London.
Abstract:
Some physicists surmise that gravity lies outside of quantum mechanics. Thus theories like the standard semiclassical theory of quantum to gravity coupling (that of Rosenfeld and Møller) are possible real models of interaction, rather than a mere approximation of a theory of quantum gravity. Unfortunately, semiclassical gravity creates inconsistencies such as superluminal communication. Alternatives by authors such as Diósi, Martin, Penrose, and Wang often use the term ’stochastic’ to set themselves apart from the standard semiclassical theory. These theories couple to fluctuations caused by for instance continuous spontaneous localization, hence the term ’stochastic’. This paper looks at stochastic gravity in the framework of a class of emergent or ontological quantum theories, such as those by Bohm, Cetto, and de Broglie. It is found that much or all of the trouble in connecting gravity with a microscopic system falls away, as Einstein’s general relativity is free to react directly with the microscopic beables. The resulting continuous gravitational wave radiation by atomic and nuclear systems does not, in contrast to Einstein’s speculation, cause catastrophic problems. The small amount of energy exchanged by gravitational waves may have measurable experimental consequences. A very recent experiment by Vinante et al. performed on a small cantilever at mK temperatures shows a surprising non-thermal noise component, the magnitude of which is consistent with the stochastic gravity coupling explored here.
I’m headed to London for the EmQM 2017 conference Oct 26 – 28 2017, which will I am looking forward to.
I attended in 2015. The event has the byline – the 4th International Symposium about Quantum Mechanics based on a »Deeper Level Theory«. Its mission this year is
Towards Ontology of Quantum Mechanics and the Conscious Agent David Bohm Centennial Symposium
When I first really understood what quantum mechanics really was – in second-year undergrad at the University of Toronto, I immediately read all sorts of books and papers by and about Bohm’s theories. He made quite a change in my outlook of physics in general. I became convinced in 1985 that quantum mechanics was incomplete and that something along the lines of Bohm’s theory was the way to go. That makes the conference more special for me, and I’m sure many other attendees share the same view.
I am presenting a poster which I’m still polishing that up right now (the abstract at least was well received!). Its based on a paper called ‘Fully Classical Quantum Gravity (see link)‘. I have renamed the poster to Stochastic Gravity and Ontological Quantum Mechanics and rewritten most of it.
The poster describes the results of a paper by Vinante et al. :
Improved noninterferometric test of collapse models using ultracold cantilevers . If the results hold up, they are quite breathtaking as they state:
The finite intercept, clearly visible in the inset of Fig. 3 implies that the data are not compatible with a pure thermal noise behavior, and a nonthermal ex-cess noise is present.
The paper details the careful procedures followed to chase down possible experimental problems. The analysis is carefully thought out. The paper claims the results show a possible signature of Adler’s Continuous Spontaneous Localization (CSL), but to me it seems like if the results hold up that its simply a great puzzle to solve! My take (in line with the ‘Fully Classical Quantum Gravity‘ paper) is that this noise is caused by the continuous emission and/or absorption of gravitational waves at nuclear frequencies.
Gravitational waves are notoriously hard to see, and these high-frequency ones (HFGWs) even more so. Indeed, since gravitational wave power goes with the square of frequency, truly tiny values of the gravitational wave strain ‘h’ (h == 0 in flat space and h < 1) make for large energy fluxes. The LIGO observations saw gravitational waves with 
So LIGO can see gravitational waves with a flux of about 
Another way of thinking about this result is that anytime a better telescope is built, or one is built that looks at a new wavelength, field or pattern of signals, those signals are not only discovered, they produce deep new insights about our universe. The fact that HFGWs are hard to detect does not mean that they are not there! Indeed, instead of calculating what the flux of HFGWs might be around us, we should instead admit our ignorance and calculate what we don’t know. Huge amounts of gravitational wave energy could be whipping by everything right now and we would not know a thing about it.
It’s going to be a quick few days in London!
–Tom
I have been reading up on the trans-Planckian problem with the black hole evaporation process. (See the end for an update in March 2018)
Here is the problem.
An observer far away from a black hole sees photons of normal infared or radio wave energies coming from a black hole (i.e. << 1eV). If one calculates the energies that these photons should have once they are in the vicinity of the black hole horizon, the energy is becomes high – higher than the Planck energy, exponentially so. Of course if we ride with the photon down to the horizon, the photon blue shifts like mad, going ‘trans-Planckian’ – i.e. having more energy than the Planck energy.
Looked at another way: if a photon starts out at the horizon, then we won’t ever see it as a distant observer. So it needs to start out just above the horizon where the distance from the horizon is given by the Heisenberg uncertainty principle, and propagate to us. The problem is that the energy of these evaporating photons must be enormous at this quantum distance from the horizon – not merely enormous, but exponentially enormous. A proper analysis actually starts the photon off in the formation of the black hole, but the physics is the same.
Adam Helfer puts it well in his paper. Great clear writing and thinking.
Trans–Planckian modes, back–reaction, and the Hawking process
Helfer, A. D. (2000). Trans–Planckian modes, back–reaction, and the Hawking process. Retrieved from https://arxiv.org/pdf/gr-qc/0008016.pdf See also See Helfer, A. D. (2005). Quantum Character of Black Holes. Retrieved from https://arxiv.org/pdf/gr-qc/0503053.pdf
My take is simple. After reading Hefler’s paper plus others on the subject, I’m fairly convinced that black holes of astrophysical size (or even down to trillions of tons) do not evaporate.
The math is good. The physics isn’t
Let’s get things straight here: the math behind Hawking evaporation is good: Hawking’s math for black hole evaporation is not in question.
It should be emphasized that the problems uncovered here are entirely physical, not mathematical. While there are some technical mathematical concerns with details of Hawking’s computation, we do not anticipate any real difficulty in resolving these (cf. Fredenhagen and Haag 1990). The issues are whether the physical assumptions underlying the mathematics are correct, and whether the correct physical lessons are being drawn from the calculations.
Yet Hawking’s prediction of black hole evaporation is one of the great predictions of late 20th century physics.
Whether black holes turn out to radiate or not, it would be hard to overstate the significance of these papers. Hawking had found one of those key physical systems which at once bring vexing foundational issues to a point, are accessible to analytic techniques, and suggest deep connections between disparate areas of physics. (Helfer, A. D. (2003). Do black holes radiate? Retrieved from https://arxiv.org/pdf/gr-qc/0304042.pdf)
So it’s an important concept. In fact it so important that much of not only black hole physics but quantum gravity and cosmology all use or even depend on black hole evaporation. Papers with titles like “Avoiding the Trans-Planckian Problem in Black Hole Physics” abound.
The trans-Planckian problem is indicative of the state of modern physics.
There are so many theories in physics today that rely on an unreasonable extrapolation of the efficacy of quantum mechanics at energies and scales that are not merely larger than experimental data, but exponentially larger than we have experimental evidence for. Its like that old joke about putting a dollar into a bank account and waiting a million years – even at a few per cent interest your money will be worth more than the planet. A straightforward look at history shows that currency and banks live for hundreds of years – not millions. The same thing happens in physics – you can’t connect two reasonable physical states through an unphysical one and expect it to work.
The trans-Planckian problem is replicated perfectly in inflationary big bang theory.
The trans-Planckian problem seems like a circle the wagons type of situation in physics. Black hole evaporation now has too many careers built on it to be easily torn down.
Torn down:
To emphasize the essential way these high–frequency modes enter, suppose we had initially imposed an ultraviolet cut–off Λ on the in–modes. Then we should have found no Hawking quanta at late times, for the out–modes’ maximum frequency would be ∼ v′(u)Λ, which goes to zero rapidly. (It is worth pointing out that this procedure is within what may be fairly described as text–book quantum field theory: start with a cut–off, do the calculation, and at the very end take the cut–off to infinity. That this results in no Hawking quanta emphasizes the delicacy of the issues. In this sense, the trans–Planckian problem may be thought of as a renormalization–ambiguity problem.)
Some may argue that other researchers have solved the trans-Planckian problem, but its just too simple a problem to get around.
One way around it – which I assume is what many researchers think – is that quantum mechanics is somehow different than every other physical theory ever found, in that it has no UV, IR, no limits at all. In my view that is extremely unlikely. Quantum mechanics has limits, like every other theory.
Possible limits of quantum mechanics:
- Zero point: Perhaps there is a UV cut – ( Λ ) . The quantum vacuum cannot create particles of arbitrarily large energies.
- Instant collapse. While its an experimental fact that QM has non-local connections, the actual speed of these connections is only tested to a few times the speed of light.
- Quantum measurement – Schrödinger’s cat is as Schrödinger initially intended it to be seen – as an illustration of the absurdity of QM in macroscopic systems.
If there is a limit on quantum mechanics – that QM is like any other theory – a tool that works very well in some domain of physical problems, then many many pillars of theoretical physics will have to tumble, black hole evaporation being one of them.
The other argument – Unruh saves evaporation?
March 2018 update: Ok – upon reading this paper by Steven B. Giddings
Where does Hawking radiation originate? A common picture is that it arises from excitations very near or at the horizon, and this viewpoint has supported the “firewall” argument and arguments for a key role for the UV-dependent entanglement entropy in describing the quantum mechanics of black holes. However, closer investigation of both the total emission rate and the stress tensor of Hawking radiation supports the statement that its source is a near-horizon quantum region, or “atmosphere,” whose radial extent is set by the horizon radius scale.
So after I wrote this I am not convinced that holes don’t radiate.
Adam’s argument is below. Basically in order for Unruh’s/Giddings ‘saving’ of black hole radiation to work, there has to be enough ‘source space’ around the black hole to generate the Hawking radiation. There might be.
Qingdi Wang, Zhen Zhu, and William G. Unruh
It (I will call the paper WZU) has been discussed at several places:
Sabine Hossenfelder at the Backreaction blog,
Reddit ,
So why talk about it more here?
Well because its an interesting paper, and I think that many of the most interesting bits have been ignored or misunderstood (I’m talking here about actual physicists not the popular press articles).
For instance here are two paragraphs from Sabine Hossenfelder
Another troublesome feature of their idea is that the scale-factor of the oscillating space-time crosses zero in each cycle so that the space-time volume also goes to zero and the metric structure breaks down. I have no idea what that even means. I’d be willing to ignore this issue if the rest was working fine, but seeing that it doesn’t, it just adds to my misgivings.
So with the first paragraph, Sabine is talking about the a(t, x) factor in the metric (see equation 23 in the paper). I think that she could be a little more up front here: a(t, x) goes to zero alright, but only in very small regions of space for very short times (I’ll come back to that later). So in reality the average of the a(t,x) over any distance/time Planck scale or larger determines an almost flat, almost Lambda free universe -> average(a(t,x)) –> the a(t) as per a FLRW metric. I guess Sabine is worried about those instants when there are singularities in the solution. I agree with the answer to this supplied in the paper:
It is natural for a harmonic os- cillator to pass its equilibrium point a(t,x) = 0 at maximum speed without stopping. So in our solution, the singularity immediately disappears after it forms and the spacetime continues to evolve without stopping. Singularities just serve as the turning points at which the space switches. ...(technical argument which is not all that complicated)... In this sense, we argue that our spacetime with singularities due to the metric becoming degenerate (a = 0) is a legitimate solution of GR.
As I said, more on that below when we get to my take on this paper.
The second paragraph above from the Backreaction blog concerns the fact that the paper authors used semi classical gravity to derive this result.
The other major problem with their approach is that the limit they work in doesn’t make sense to begin with. They are using classical gravity coupled to the expectation values of the quantum field theory, a mixture known as ‘semi-classical gravity’ in which gravity is not quantized. This approximation, however, is known to break down when the fluctuations in the energy-momentum tensor get large compared to its absolute value, which is the very case they study.
They are NOT using a classical gravity coupled to the expectation values of the quantum field theory. Indeed, according to WZU and the mathematics of the paper they say:
In this paper, we are not trying to quantize gravity. Instead, we are still keeping the spacetime metric a(t, x) as classical, but quantizing the fields propagating on it. The key difference from the usual semiclassical gravity is that we go one more step—instead of assuming the semiclassical Einstein equation, where the curvature of the spacetime is sourced by the expectation value of the quantum field stress energy tensor, we also take the huge fluctuations of the stress energy tensor into account. In our method, the sources of gravity are stochastic classical fields whose stochastic properties are determined by their quantum fluctuations.
So I think that she has it wrong. In her reply to my comment on here blog she states that its still semiclassical gravity as they use the expectation values of the fluctuations (they don’t as you can see by the quote above or better by looking at the paper. See how the equation 29 talks about expectation values, but the actual solution does not use them ). She concludes her comment: “Either way you put it, gravity isn’t quantized.” I think that’s also fair appraisal of the attitude of many people on reading this paper many people don’t like it because gravity is treated classically.
Why I think the paper is interesting.
Gravity is not quantized: get over it
I think its interesting as their approach to connecting gravity to the quantum world is basically identical to my Fully Classical Quantum Gravity experimental proposal – namely that gravity is not quantized at all and that gravity couples directly to the sub-quantum fluctuations. Wang and co-authors apologize for the lack of a quantum theory of gravity, but that appears to me anyway as more of a consensus-towing statement than physics. Indeed, the way its shoved in at the start of section C seems like it is an afterthought.
(Gravitational) Singularities are no big deal
Singularities are predicted by many or (even all?) field theories in physics. In QED the technique of renormalization works to remove singularities (which are the same as infinities). In the rest of modern QFT singularities are only perhaps removed by renormalization. In other words quantum field theory blows up all by itself, without any help from other theories. Its naturally bad.
The Einstein equations have a different behaviour under singular conditions. They are completely well behaved. Its only when other fields are brought in, such as electromagnetism or quantum field theory that trouble starts. But all on their own singularities are no big deal in gravity.
So I don’t worry about the microscopic, extremely short lived singularities in WZU at all.
Why it’s exciting
We have WZU metric equation 23
ds2 = −dt2 +a2(t,x)(dx2 +dy2 +dz2)
a(t,x) oscillates THROUGH zero to negative, but the metric depend on a^2, so we have a positive definite metric that has some zeros. These zeros are spread out quasi periodically in space and time. If one takes two points on the manifold (Alice and Bob denoted A & B), then the distance between A and B will be equivalent to the flat space measure (I am not looking at the A and B being cosmic scale distances apart in time or space, so its almost Minkowski). Thus imagine A and B being 1 thousand km apart. The scale factor a(t, x) averages to 1.
Here is the exciting bit. While an arbitrary line (or the average of an ensemble of routes) from A -> B is measured as a thousand km, there are shorter routes through the metric. Much shorter routes. How short? Perhaps arbitrarily short. It may be that there is a vanishingly small set of paths with length ds = 0, and some number of paths with ds just greater than 0, all the way up to ‘slow paths’ that spend more time in a > 1 areas.
Imagine a thread like singularity (like a cosmic string – or better a singularity not unlike a Kerr singularity where a >> m). In general relativity such a thread is of thickness 0, and the ergo region around it also tends to zero volume. One calculation of the tension on such a gravitational singularity ‘thread’ (I use the term thread as to not get confused with string theory) come out to a value of about 0.1 Newtons. A Newton of tension on something so thin is incredible. Such a thread immersed in the WZU background will find shorter paths – paths that spend more time in areas where a << 1, these paths being much more energetically favoured. There are also very interesting effects when such gravitational thread singularities are dragged through the WZU background. I think that this might be the mechanism that creates enough action to generate electromagnetism from pure general relativity only.
A 2D slice at some time through ordinary WZU vacuum. The spots are places where a~2. The straight line from A to B has an average scale factor a of 1, while the wiggly path follows a ~ 0 and hence has an average scale factor of << 1. Note that these short paths are not unique, and there is little constraint for them to be even approximately straight.
So these thread singularities thread their way through the frothy WZU metric and as such the distance a single such thread may measure between Alice and Bob may be far far less than the flat space equivalent.
It seems to me that one could integrate the metric as given in WZU equation 23 with a shortest path condition and come up with something. Here is one possible numerical way: start out with a straight thread from A to B. Then relax the straight line constraint, assign a tension to the thread, and see what the length of the thread after a few thousand iterations, where at each iteration, each segment allows itself to move toward a lower energy state (i.e. thread contraction).
This opens up:
Quantum non-locality
Realist, local quantum mechanics is usually thought of requiring on having some dependency on non-local connections, as quantum experiments have shown. This shortcut path may be an answer to the need for non-local connections between particles, i.e. a mechanism for entaglement, a mechanism for Einstein’s “spooky action at a distance”.
Faster than light communication.
Its always fun to see if there are realistic methods where one might beat the speed limit on light. It seems that worm hole traversal has been one of the favourites to date. I think that the WZU paper points at another mechanism – the fact that there exist shorter paths through the sub-quantum general relativistic froth of WZU. How might one construct a radio to do this? Entangled particles, particles that follow the zeros of a(t, x) preferentially, etc etc. One could imagine a brute force method to test this where huge pulses of energy are transmitted through space at random intervals. Perhaps a precursor signal could be measured at the detector, where some of the energy takes a short path through the WZU metric.
Emergent quantum mechanics comes in many forms: stochastic electrodynamics ( Ana María Cetto) , de Broglie – Bohmian mechanics (John W M Bush) , thermal models ( Gerhard Groessing ) etc. In many of these forms of emergent quantum mechanics, particles have a physical existence and experience sub quantal movement. The paper I have just posted looks at the gravitational consequences of this sub quantal motion. An interesting finding is that while a classical Bohr hydrogen atom has a lifetime of about 10^-11 seconds, it would take that same atom 10^40 seconds or so to radiate away a few eV of energy. This indicates that the stability of the atoms is not an indication that gravity needs to be quantized, which is antithetical to Einstein in 1916:
- “…Nevertheless, due to the inner-atomic movement of electrons, atoms would have to radiate not only electro-magnetic but also gravitational energy, if only in tiny amounts. As this is hardly true in Nature, it appears that quantum theory would have to modify not only Maxwellian electrodynamics, but also the new theory of gravitation.” – Einstein, 1916
Einstein it would seem was wrong on the gravtitational side of this.
Working Paper Fully Classical Quantum Gravity
The paper looks at possible ways to see these tiny emissions (nuclear scale emissions are higher) and thus lays out a quantum gravity experiment achievable with today’s technology.
The experimental parameter space. Most important thing to note is that this is a quantum gravity experiment with an achievable parameter space!
Here is the paper…
Also see these references…
Article Emergent Quantum Mechanics
Abstract
(This article is a work in progress…)
We posit that the de Broglie wave as a real physical wave produced by interactions between any massive particle and the gravitational background zero point field.
de Broglie waves are tied to momentum. They are associated with any free particle. For instance an electron or a Buckyball. In my view they are some sort of beat phenomenon – doppler effect.
There is a huge background of Gravitational waves at some very large frequency – (perhaps Planckian).
How physically would waves associate with every single mass ? The only possible coupling is through mass itself. So what is the result of something the mass of an electron on a homogenous gravitational wave background?
The mass will distort the background wave pattern.
From this distortion would come some sort of interference pattern. Think of the rubber mat analogy. There would be a dent for the electron in a sea of waves. Would this effect a much much lower frequency effect – de Broglie waves -?
If we take the mass of the particle as m, and the frequency of the background waves as 1.85e43 Hz. Perhaps this gives us the ‘dark energy’, along with quantum guidance rules.
Introduction
The de Broglie wave is a wave that can be used to predict the quantum behaviour of particles. Its a wavelength that is tied to momentum.
The de Broglie wavelength is the wavelength, λ, associated with a massive particle and is related to its momentum, p, through the Planck constant, h:
This wave seems puzzling. Its tied to momentum, so for an observers travelling with different velocities will measure different de Broglie wavelengths. This is often taken as an indication of the non – reality of these waves. But there is a simple explanation for this – and its based on special relativity.
de Broglie beats and the Compton frequency:
"de Broglie made a second, less well known conjecture. If you combine the E=mc2 and the E=hf equations (where f is frequency), you arrive at the Compton frequency. de Broglie's conjecture was that the Compton frequency reflected, in the case of the electron (quarks were not yet discovered), some kind of fundamental intrinsic oscillation or circulation of charge associated with the electron. However it is now known that this presumed oscillation can also be interpreted instead as being externally driven by the zero-point fluctuations of the quantum vacuum (see chap. 12 of the monograph "The Quantum Dice" by de la Pena and Cetto). Now comes a very intriguing result. One can easily show that if the electron really does oscillate at the Compton frequency in its own rest frame, when you view the electron from a moving frame a beat frequency becomes superimposed on this oscillation due to a Doppler shift. It turns out that this beat frequency proves to be exactly the de Broglie wavelength of a moving electron." http://www.calphysics.org/mass.html
There is still a problem though. The de Broglie relationship holds for any object, experimentally measured up to a Buckyball with hundreds of component particles. Thus the de Broglie wavelength is some effect of mass combined with motion. The only effect that mass has on a purely classical geometric world is the Schwarzschild ‘indent’ on the background space time.
So how can an indent give rise to a beat frequency?
This result may be generalized to include ZPF radiation from all other directions, as may be found in the monograph of de la Pena and Cetto [5]. They conclude by stating: “The foregoing discussion assigns a physical meaning to de Broglie’s wave: it is the mod-ulation of the wave formed by the Lorentz-transformed, Doppler-shifted superposition of the whole set of random stationary electromagnetic waves of frequency ωC with which the electron interacts selectively.”
Assume some white noise like stochastic gravitational wave spectrum as a background on that exists everywhere in the universe (as it undoubtedly does, with only the amplitude unknown). What is the result of viewing a truncated Schwarzschild solution moving (say slowly to ease the math at first) through this background?
One would expect lensing of this stochastic field. The field will refract modes that match its characteristic size. This size scales to its mass. First consider a particle at rest with respect to the observer. With the dent this causes in space time we see a time dilation which affects the waves cumulatively, causing an internal Compton frequency – which is a result of the
Another solution as explained by Rober Schuler
There is an obvious heuristic, however, which provides the needed frequency sum to a good approximation. We need only assume that, like Schrödinger waves, de Broglie waves are related to the probability of finding a particle. Let p(A) be the probability of finding A, and p(B) the probability of finding B, and assume these meanings continue to hold if A and B are bound together. One of the interesting aspects of de Broglie’s paper (actually his thesis, which was printed in a journal), is a section treating bound particles where both are considered to be moving. [Ibid. 12] By contrast, when using Schrödinger’s analysis, stationary confinement boundaries and potentials are used (which would be associated with particles, e.g. a stationary nucleus, that have infinite de Broglie wavelength). Since we are only able to find the bound pair AB if we find both A and B, then the probability of finding AB must be p(AB) = p(A)p(B). If “p” is a sinusoidal function, then indeed the product of two such functions reduces by a common trig identity to a term involving the sum of the frequencies of p(A) and p(B), and a term involving their difference. The sum frequency corresponds perfectly to the frequency of the sum of the masses of A and B. The only problem is what to do with the difference frequency? Wignall’s method was speculative, and we can’t use it anyway because he was not using probability, but complex valued functions. However, as an approximation we can observe two things. First, in the case of common nuclear particles, whether we treat them as hadrons (protons, neutrons), or quarks, the masses are approximately the same and the difference frequencies are therefore approximately zero. Second, in the case of the binding of electrons to a nucleus, the electron mass is to a good approximation negligible. It
Once this relationship is obtained, the de Broglie matter waves are a necessary conclusion, as the literature indicates.
So one is left with the task of showing that any truncated Schwarzschild solution will cause an internal frequency – a mode trap – when its sitting in a stochastic gravitational field.
The next step
Assume standing GR waves (in well defined the universal rest frame). 1.85e43 Hz. Then there is a Schwarzschild solution sitting in that standing wave bath.
Time dilation lapse function sqrt(1- 2M/r) becomes simply 1-M/r unless you are within 1e-30m of an electron. So that is the lapse function. What beat frequency does our planckian background generate ? – The compton frequency. Redshift.
https://en.wikipedia.org/wiki/Gravitational_redshift – there are
Take equation for z (r -> inf) and mult by the huge planck frequency. You then get the compton frequency. Solve the equation for the radius of the electron and get the planck length. (But this requires that the electron is quite small and that the buckyball is even smaller! – also this calculation is for a monochromatic wave – not a stochastic background). What about using the width of the
So that is the size of the electron. One planck size will give you a gravitational (blueshift from outside) of the compton electron frequency.
https://en.wikipedia.org/api/re
st_v1/media/math/render/svg/d50a640dc99823e7f650b0c2580ec3bc51ea7ddd
Coulomb Attraction
de Broglie
The proton de Broglie frequency is about the exact same number –
“He asserted that quantum mechanics was intrinsically relativistic and proposed that the pilot wave originates in internal particle oscillations at the Compton frequency, ωc =mc2/h ̄, at which rest mass energy is exchanged with wave energy. He proposed that the guiding wave field evolves according to the Klein-Gordon equation and consists of a monochromatic wave field in the particle’s frame of reference. The de Broglie relation, p = h ̄ k, then relates the particle momentum to the de Broglie wavelength, λdB = 2π/k. Finally, he stressed the importance of the harmony of phases, by which the particle’s internal vibration, seen as that of a clock, stays in phase with its guiding wave (de Broglie 1930, 1987). Thus, according to his conception, the wave and particle maintain a state of resonance.” [reference]
and try to find your friend at the other end.” — Leonard Susskind
In this talk Leonard Susskind gives a convincing argument as to why he th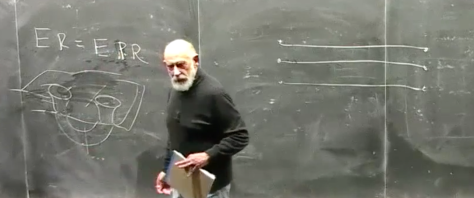
inks that ER == EPR , where ER denotes an Einstein – Rosen Bridge (aka wormhole) and EPR is the Einstein Podolsky Rosen paper (essentially entanglement).
Leonard draws three entangled pairs of particles on the chalkboard, (image its not merely 3 by 3e40) and then collapse the left and right down to black holes, then the entaglement must continue, and thus ER == EPR
The classical gravitational radiation of Atoms:
Over the course of the lifetime of the universe, the Hydrogen atom releases 8 eV of energy as gravitational waves. So if its in a bath of these waves, then the loss would be much less – virtually zero.
For large atoms one would think that this energy exchange would be bigger. Of course ‘the actual path’ of the electron matters. The base energy level of an electron
Einstein in 1916 when wrote:
“Nevertheless, due to the inner-atomic movement of electrons, atoms would have to radiate not only electro-magnetic but also gravitational energy, if only in tiny amounts. As this is hardly true in Nature, it appears that quantum theory would have to modify not only Maxwellian electrodynamics, but also the new theory of gravitation.”
Why did Einstein worry about something that would effect the lifetime of an atom on time scales of the universe vs the tiny amount of time that a classical hydrogen at radiates EM energy?
Possibility of measuring something here.
- Get a lot of heavy atoms in ‘sync’ (NMR?)
- Radiating some amount of GR away, perhaps measure that on another bunch of similarly prepared atoms?
- ??? likely nothing…?
Also related — ? http://arxiv.org/abs/0708.3343 Thermal gravitational waves. 80 MW from the Sun, from atoms sliding near each other.
Its also easy to see that the resulting model is fully compatible with relativity and GR. Its after all made entirely out of gravity.
Calculation – watts emitted from one mole of uranium atoms (~200 grams of
uranium
)
- Use formula for watts emitted by a rod of mass m rotating at a frequency.
- http://www.twinkletoesengineering.info/atoms.htm
- So the uranium inner orbit has a velocity of 0.5c and a radius 1/8 that of hydrogen
- http://www.wolframalpha.com/input/?i=(0.5*c)%2F(2*pi*(hydrogen+atom+radius)%2F8)
- So we have 7.3e18 Hz and a radiative power of 10^-23 watts
Take this radiated power, and assume that uranium is thus in a bath of GR waves at 10^19 hz, so that it emits on average the same amount that it absorbs, (like SEDs only a lot easier to imagine).
Experiment: Now take a semi-sphere of uranium and put a test mass in the middle. If its uranium (i.e. tuned to the neighbouring shell) it will feel some force, but if its something with a different material and hence different frequency pattern of gravitational waves, it will not feel the force from the shell. Better experiment: Two massive plates, one uranium or lead, the other with a different material of same mass but different inner orbital frequencies. Then hook up one of those torsion threads to two balls on an arm, one of each material, and look for a rotational force. (Using some with force materials).
Classical Nucleus – nucleus GW interaction.
Iron nucleus – speed of nucleons is (20 MeV kinetic energy) and say one pair is radiating Gravitational waves: r = 1 fm, so
I get about 1e-25 watts or so. (using this) . Model is that nucleons are moving about in the nucleus, and at times have a quadrupole motion, which is on the order of a bar of mass 2 nucleons, spinning about a fm apart at the 10^23 hz of the nucleon rotational period in a fermi gas model nucleus. (Note that the Sivaram and Arun paper about thermal gravitational radiation from neutron stars shows about a billion times less than this.
Taking 1e-25 watts – which is 10e-7 eV/second I can calculate the pressure between two 10kg masses 0.1 metres apart, I get 10^-10 newtons. This is about the right amount of effect to mess up all the newtonian gravitational constant experiments.
Using Pressure = E/c , where E is in Watts/metres^2 and 1e-25 watts per nucleon emitted, assume complete absorption. (not cross section is assumed about the physical size of the nucleon, which is also the gravitational wavelength). Then we get the 10^-10 newtons.
Gravity force between 2 10kg masses at 0.1 apart is 6.7e-7 Newtons.
This force is not the nuclear strong force or the electromagnetic force, (which are stronger) but simply assuming that the nucleus can be treated classically for gravitational waves. The nucleons generate GWs which are can be absorbed by another nucleon of the same kind.
A couple of months ago I read Jim Baggot’s Farwell to Reality. I was very impressed. I won’t go into details, but the book takes the eminently reasonable suggestion that 11 dimensions, uncountable infinities of universes and other mainstream theoretical physics subjects are “fairy tale physics”. Physics really needs people like Jim Baggot, Peter Woit, and Lee Smolin to show that the emperor has no clothes. But what if things are far worse than these authors report?
So I went looking for other writing critical of modern physics. Did I find it. I read two of Alexander Unzicker’s books. The Higgs Fake and Bankrupting Physics. They are a great read, whether you agree with him or not(caution – unintended hilarity). As if to underline the mindset of the physics community at large, after writing these two books Unzicker had trouble with arXiv, and has several more stories about the negative reaction of this closely knit society to outside criticism. One fact about criticism is that people get most upset when the criticism strikes close to the truth. Peter Woit’s criticism of Bankrupting Physics revolves around trying to classify Unzicker as ‘a garden-variety crank’ – which of course then makes Woit’s job easy as it automatically discounts everything he says (unless he is in agreement with Woit of course). My take is simpler: Woit’s book and blog regularly complains about string theory and the multiverse being bunk, which in my opinion is something like 99.9999% likely to be true, while Unzicker’s assertions are ‘only’ 10 – 99.9999% likely to be true. Contrast that with the 50,000 papers on supersymmetry – each one of which is a 100% waste of time according to both Woit and Unzicker. Peter Woit can be wrong too. There are other areas of physics that smell as bad as String Theory.
Physics is broken. Worse than we think.
Eureka!
The Ligo measurement is the greatest thing to happen in Physics and Astronomy for decades. Amazing work. It was about 50 years ago that the first gravitational wave detector was built by Weber. It took 50 years of refinement, many PhDs postdocs and full careers, but the LIGO team did. it.
I will assume that you have already read the paper and other popular sources on this observation, so I will jump into what excites me about this observation:
The enormous gravitational wave energy emitted.
How much energy? Three solar masses worth of gravitational waves were emitted over just a few tenths of a second. The paper reports a peak gravitational energy emission of 200 solar masses per second! See the paper for errors on this estimate but its accurate to within 20%. The really amazing thing though is that this emission took place from a region only about 200 km across. The frequency of the waves at peak emission is (from the paper fig 1 – bottom row) 120 Hz or so.
Lets look at that amount of energy in terms of another form of energy that we are more comfortable with – electromagnetic waves – light. I want to compare this to the “Schwinger limit” – which is the maximum electromagnetic field that can occur before quantum pair creation effects take over. The Schwinger limit controls the maximum power that a region of space can transmit through itself (via opposing overlapping lasers say).
Say we had standing radio waves at 120Hz in a 200km on a side box, how much power could such an area radiate if it were only limited by the Schwinger limit? (i.e. ignore the mechanism by which such spectacular amounts of energy could be turned into radio waves).
The formula for energy density given an electric wave is quite simple: See for instance this hyper physics page:
Total Energy density = ε*E2 So at the Schwinger limit of 1.3×1018 V/m and with the constant ε being 8.854187817620… × 10-12 Farads/m, we get 1.5×1025 kg/m/s2. We have 200,000 metres per side, so there are 1.2×1041 J (joules) in a 200km on a side box at the Schwinger limit.
How many joules of gravitational wave energy were held in a 200km box around GW150914? Well at 200 solar masses per second emitted, we need to take the size of the box and use light travel time to determine the amount of energy in the box at any one time: So 200 solar masses per second. Light travel time is 200km/(3e8m/s) = 6.7×10-4 seconds. So if that volume emits 200 solar masses of energy per second, then that is 0.13 solar masses worth of energy at any one time in that volume, or 2.3×1046 Joules! This is some 5 orders of magnitude above what can be emitted by this same region using electromagnetic means!
Discussion
The mechanism by which one arrives at the Schwinger limit is conceptually simple – ‘QED non linear photon – photon scattering’ involving electron – positron pair 
creation. (See the wikipedia article for a start).
Is there a corresponding quantum ‘Schwinger limit’ for gravitational waves (gravitons)? Well there is of course a limit in place due to classical general relativity, which is well known. In this case we are close (gravitational h is about 0.001 or so?) of the classical limit, which is basically that you can’t pile anything up so that the density would cause a black hole to form. But is there a feynman diagram for graviton – graviton scattering – well of course there is – it should behave like real classical gravity! I guess what I am wondering – is there another pathway where graviton scattering would take place and according to QM make the GW150914 ‘impossible’?
Does the observation of gravitational waves 5 orders of magnitude stronger than the strongest possible electromagnetic wave mean that we can finally stop calling gravity the weakest force? Yes to that!
My take as anyone who reads any of this site will know is that electromagnetism, quantum mechanics and the nuclear forces are all emergent phenomena from classical general relativity (see my poster). To me this observation is another hint at what general relativity can do.
As a further note, this corresponds to 0.018 watts per square metre at the 1.3 billion LY distance of the earth! That means that the earth had 2.3 Terawatts of gravitational energy passing through it on Sept 14 2015, just from this one event. Yet this massive amount of power is barely within observational limits of LIGO. LIGO sees only nice correlated bumps (with only 2 detectors its not really built to look at the background of gravitational wave energy), so we could easily have this much energy passing through the earth in the form of these stochastic low frequency gravitational waves all the time, and LIGO would not be able to detect it.
Gravitational waves make the perfect sub-quantum excitation – they can carry very large amounts of energy without anything but a carefully designed detector being able to pick them up.
What would be an ideal detector for LIGO frequency waves?
Other than the actual LIGO observatory of course (which I argue below may not be the ideal gravitational wave detector).
A nice isolated black hole maximally spinning at near a = 1, and of the same approximate mass as the GW150914 emitter would exchange a substantial amount of the incoming wave energy into motion – and it would pick up something like 0.2 GW of power for a fraction of a second, which would likely be observable since this hypothetical black hole is sitting so nice and quiet, a GJ of energy exchange would cause small (since the thing is so heavy) but measurable effects.
Say we don’t have a nearby system (we would need varying sizes to couple to the frequencies we wish to monitor) of quiet black holes to listen to. What else could we build? The ideas opens up if one assumes that matter and light are both gravitational phenomena. What would be ideal is something that mimics a tuned superradiant like interaction with gravitational waves, but it trillions of times lighter and made of ‘ordinary matter’. What makes super radiance work?
http://serious-science.org/superradiance-in-ultracold-molecular-samples-4343
“What happened is that because this Rydberg atom stayed very high excited, but up there the energy levels are very-very close together. What does that mean? The transitions have very long wavelengths. So basically every sample that you can have is very small compared to these long wavelengths. And so superradiance is actually quite likely in these cases. And this is actually exactly what happened. As I said, it was an accident, I don’t think it could have been done such an ideal experiment on purpose in this case.”
Andersen, T. C. on ORCID
General Relativity 